Le grandezze vettoriali
Nello studio della teoria della vela avremo continuamente a che fare con forze e velocità. Le forze di cui parliamo sono quelle derivanti dalla interazione della barca col vento e con l’acqua; le velocità sono quelle proprie del vento, dell’acqua e della barca stessa. Tanto le une quanto le altre sono grandezze che non possono essere completamente definite solo specificando una dimensione (modulo) ma richiedono che siano indicati anche una direzione ed un verso rispetto ad un sistema di riferimento. I vettori sono comunemente usati per indicare grandezze di questo tipo che sono quindi chiamate grandezze vettoriali, in contrapposizione alle grandezze definite “scalari” che sono caratterizzate unicamente da una misura (magnitudine). Sono tali ad esempio i pesi, i volumi, i valori monetari, etc.
Le operazioni basilari (+/-) su grandezze semplici (scalari), si risolvono con le normali operazioni aritmetiche. Le stesse operazioni, quando intervengono su vettori, richiedono operazioni più complesse che coinvolgono tutti i parametri che li caratterizzano, salvo qualche eccezione.
L’importanza di considerare correttamente le velocità e le forze come vettori, dipende dalla frequente necessità di eseguire mentalmente e “al volo” somme e sottrazioni di queste grandezze.
La soluzione numerica di queste operazioni richiede strumenti di matematica superiore ma fortunatamente quelle che ci interessano possono facilmente essere risolte graficamente. Chi avesse sostenuto l’esame per la patente nautica, nella prova di carteggio ha sicuramente eseguito graficamente somme o sottrazioni di vettori-velocità per calcolare una rotta in presenza di corrente o scarroccio*.
Considerato che per i nostri scopi non occorre precisione nel risultato ma solo una idea visuale dello stesso, una volta compreso il metodo “carta e matita”, diventerà presto automatico visualizzare mentalmente l’operazione (grafica) ed il suo risultato. Vediamo in pratica come fare:
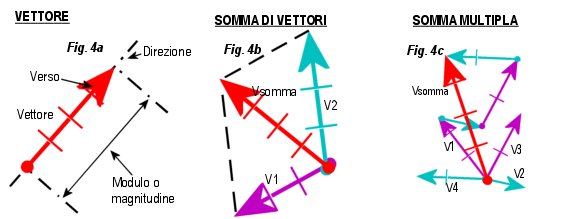
- la rappresentazione grafica di un vettore è una freccia in cui la lunghezza rappresenta il modulo (la dimensione), la linea la direzione e la cuspide il verso (fig. 4a);
- la somma di due vettori è rappresentata graficamente dalla diagonale del parallelogramma disegnato utilizzando quali lati i due vettori da sommare (fig. 4b);
- il risultato della somma di due vettori quindi sarà un terzo vettore che avrà generalmente intensità e direzione diverse da entrambi gli addendi;
- solo se la direzione degli addendi fosse uguale, sarebbe conservata nel risultato e il modulo sarebbe rappresentato dalla somma algebrica dei moduli;
- se i vettori da sommare fossero più di due si procede sommando i primi due, poi sommando il terzo al risultato e così via, oppure, più semplicemente accodandoli l’uno all’altro (fig. 4c).